Tartalom:

 

A gravitációs erő (G)

  • Isaac Newton (1642-1727) a Hold és egy alma mozgását megfigyelve arra jött rá, hogy a testek a tömegüknél fogva vonzzák egymást. Ez az erő tartja Föld körüli pályán a holdat és emiatt esik az alma a Föld felé.
  • Ezt fogalmazza meg az általános tömegvonzás törvénye, mely szerint két test között ható gravitációs erő egyenesen arányos a két test tömegével és fordítottan arányos a köztük lévő távolság négyzetével:
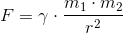
  • γ-val (gamma) jelöljük a gravitációs állandót. Értékét először Henry Cavendish mérte meg, majd Eötvös Lóránd pontosította. Értéke:
  • Két egyenként 1 kg tömegű, egymástól 1 m távolságra lévő test közötti vonzóerő: 

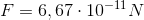
A nehézségi erő (G)

  • A gravitációs erő által a testekre kifejtett erőt nehézségi erőnek nevezzük. Jele: G
  • A gravitációs erő leegyszerűsített formája (homogén gravitációs mezővel számolunk)
  • Irányát mindig a g nehézségi gyorsulás határozza meg, ezért a legtöbb helyen nem a Föld középpontja felé mutat.
  • A vízszintes felületek mindenhol merőlegesek a nehézségi erőre.
  • Nagysága a test tömegétől (m) és a nehézségi gyorsulástól (g) függ:
  • A nehézségi gyorsulás értékei a Naprendszer égitestein:
Merkúr Vénusz Föld Hold Mars Jupiter Szaturnusz Uránusz Neptunusz
3,7 m/s2 8,87 m/s2 9,81 m/s2 1,622 m/s2 3,711 m/s2 24,79 m/s2 8,96 m/s2 8,69 m/s2 11,15 m/s2

A súlyerő

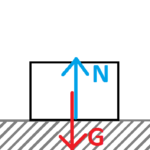
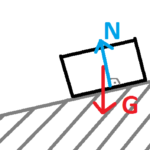
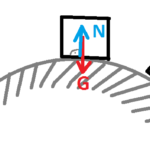
Nyomóerő (N) / felületi kényszer

  • Kényszererő
  • Támadáspont: Felületi erő -> felület közepén összpontosítjuk
  • Nagysága: alkalmazkodik; az az erő, amit a test a talajra fejt ki.
  • Iránya: merőleges a nyomott felületre:
            

Csúszási súrlódási erő (Scs)

  • Felületi erő.
  • Iránya: fékező – a sebességvektorral párhuzamos és ellentétes irányú
  • Nagysága: 
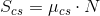
    Ahol a  μ a csúszási súrlódási együttható és az N a nyomóerő.
    A csúszási súrlódási együtthatónak nincs mértékegysége.
    Példák: http://mek.oszk.hu/00000/00056/html/082.htm
  • Iránya: ellentétes a sebesség vízszintes komponensével és párhuzamos a felülettel. (mindig fékez)

Tapadási súrlódási erő (St)

  • Az az erő, amit el kell érnünk, hogy megmozdítsuk a testet.
  • Ez az érték egyenesen arányos a nyomóerővel.
  • Nagysága: 
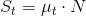
    Ahol a μ a tapadási súrlódási együttható és az N a nyomóerő.
    Általában könnyebb a csúszási súrlódás ellenében állandó sebességgel tolni (húzni) egy testet, mint a tapadási súrlódás ellenében elindítani. Ezért általában .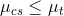
  • Iránya: ellentétes a külső erők eredőjének felülettel párhuzamos komponensével.

Kötélerő (K)

  • Ideális kötél
  • Mindkét testre ugyanakkora erő hat. 
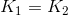
  • Mindkét testnek ugyanakkora a gyorsulása, mert össze vannak kötve: 
  • Nagysága: egy határig alkalmazkodik. (szakítási szilárdság)
  • Támadáspont: ahol húzza a testet.
  • Iránya: húzó
  • Nagyságának kiszámítása:
    • Felveszünk egy koordinátarendszert.
    • Felírjuk mind a két testre az erőket.
    • Felírjuk mindkét test X és Y komponensére a mozgásegyenletet.
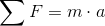
    • Tudjuk, hogy 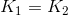  és   Végezzük el az egyenletrendszert.
      Hogyan oldjuk meg az egyenletrendszereket?

Rugóerő (R)

  • Nagysága: egyenesen arányos a rugó megnyúlásával: 
    , ahol D a rugóállandó, Δl a megnyúlás.
    A rugóállandó mértékegysége:
  • Iránya: ellentétes a megnyúlás irányával
  • Az, hogy D = 12N/cm-es rugóállandójú a rugó, azt jelenti, hogy 1 cm-rel való megnyújtáshoz R = 12N szükséges.