Mechanika – Egyenes vonalú mozgás összefoglalás
Physics, Kinematics, Mechanics
0
Jelölések
| Jelölés | elnevezés | mértékegység jele |
|---|---|---|
| x | x koordináta | m = méter |
| t | idő | s = szekundum |
| v | sebesség | m/s = méter / szekundum |
| a | gyorsulás | m/s2 = méter / szekundumnégyzet |
| Δ<jelölés> | Két időpillanat közötti változás a mértékegységek között | |
| <jelölés>0 | Egy mértékegység értéke a nulladik másodpercben. |
Egyenes vonalú egyenletes mozgás (nincs gyorsulás)
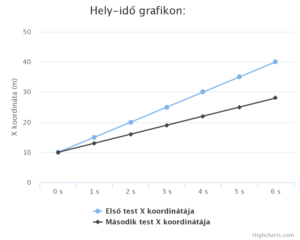
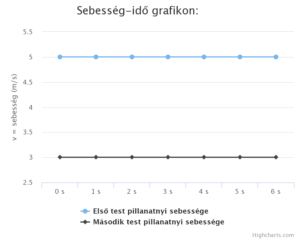
Példa adatok:
- Első test adatai:
- x0 = 10 m
- v = 5 m/s
- a = 0 m/s2
- Második test adatai:
- x0 = 10 m
- v = 3 m/s
- a = 0 m/s2
A kinematika kalkulátorral kiszámolva ezt a hely-idő grafikont és sebesség-idő grafikont kapjuk:
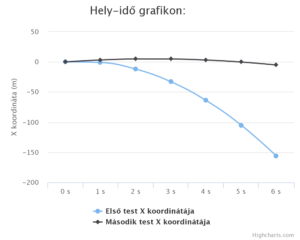
Egyenes vonalú egyenletesen változó mozgás
- A testnek a pillanatnyi sebessége másodpercenként a-val nő.
- példa adatok:
- Első test adatai:
x0 = 0 m
v0 = 4 m/s
a = -10 m/s2 = gravitáció a Földön - Második test adatai:
x0 = 0 m
v0 = 4 m/s
a = -1,62 m/s2 = gravitáció a Holdon
A kinematika kalkulátorral ezt a hely-idő grafikont és sebesség-idő grafikont kapjuk:
0
0
votes
Article Rating
Subscribe
Login
0 Comments
Inline Feedbacks
View all comments
Categories
- Cooking (1)
- Elektronika⸴ barkácsolás (6)
- Kapcsolások⸴ nyákok (3)
- Raspberry PI (2)
- Java (2)
- Physics (2)
- Electronics (2)
- Direct current (2)
- Electronics (2)
- Uncategorized (1)
- Versenyek (3)