Jelölések
| Jelölés |
elnevezés |
mértékegység jele |
| x |
x koordináta |
m = méter |
| t |
idő |
s = szekundum |
| v |
sebesség |
m/s = méter / szekundum |
| a |
gyorsulás |
m/s2 = méter / szekundumnégyzet |
| Δ<jelölés> |
Két időpillanat közötti változás a mértékegységek között |
|
| <jelölés>0 |
Egy mértékegység értéke a nulladik másodpercben. |
|
Egyenes vonalú egyenletes mozgás (nincs gyorsulás)
példa adatok:
Első test adatai:
- x0 = 10 m
- v = 5 m/s
- a = 0 m/s2
Második test adatai:
- x0 = 10 m
- v = 3 m/s
- a = 0 m/s2
A kinematika kalkulátorral kiszámolva ezt a hely-idő grafikont és sebesség-idő grafikont kapjuk:
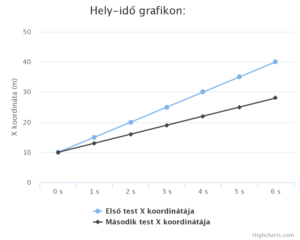 |
Figyeljétek meg, hogy a nulladik szekundumban a testek X koordinátája 10 m-nél van, ez azért van, mert az X0, azaz a kezdő x koordináta 10 méter. Az elsőtest esetében az X koordináta 5 métert növekszik, míg a második test esetében csak 3 métert. Az egyenes vonalú egyenletes mozgással haladó testek pillanatnyi helyzetét úgy határozhatjuk meg az idő (t) függvényében, hogy megszorozzuk az időt a sebességgel, majd hozzáadjuk a kezdő x koordinátát. Tehát a képlet: X(t) = v ⋅ t + x0 |
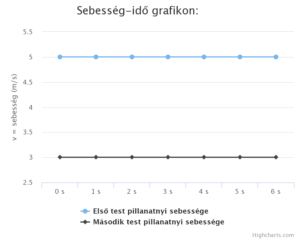 |
A sebesség-idő grafikonról leolvashatjuk, hogy egyes időpillanatokban mekkora a testek sebessége. Az első testé 5 m/s, a második testé 3 m/s. Az egyenes vonalú egyenletes mozgással haladó testek sebességet úgy határozhatjuk meg, hogy elosztjuk a Δx-et a Δt-vel:
 |
Egyenes vonalú egyenletesen változó mozgás
- A testnek a pillanatnyi sebessége másodpercenként a-val nő.
- példa adatok:
- Első test adatai:
x0 = 0 m
v0 = 4 m/s
a = -10 m/s2 = gravitáció a Földön
- Második test adatai:
x0 = 0 m
v0 = 4 m/s
a = -1,62 m/s2 = gravitáció a Holdon
A kinematika kalkulátorral ezt a hely-idő grafikont és sebesség-idő grafikont kapjuk:
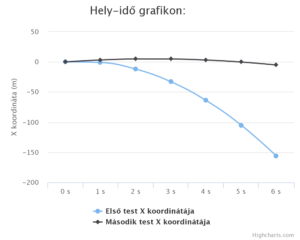 |
A hely-idő grafikonból láthatjuk, hogy a Holdon sokkal több idő kell, hogy egy test (-1,6 m/s2 gyorsulással) megtegyen egy bizonyos távolságot, mint a Földön. Egy egyenletesen gyorsuló (a = 0 m/s2) test elmozdulását úgy számolhatjuk ki, hogy a kezdősebességet (v0) megszorozzuk az idővel (t) (pont, mint az egyenletes sebességgel mozgó test esetében) és hozzáadjuk a gyorsulás felének (a/2) és az idő négyzetének (t2) szorzatát. Az elmozdulás jele s, de a ΔX is megfelelő.


|
 |
A sebesség-idő grafikonon jól látszik, hogy a -10 m/s2-tel gyorsuló test másodpercenként -10, a -1,62 m/s2-tel gyorsuló test pedig -1,62 m/s-mal növelte pillanatnyi sebességét.
A pillanatnyi sebesség kiszámításához ezt a képletet használjuk:
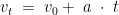
|
Kinematika feladatok




